mapa conceptual referente al calculo.

calculo avanzado. 

calculo mental con sumas.

calculo infinitesimal.

imagen de un ejercicio de calculo.

una parte de la historia del calculo en general

definición de derivadas:

Las derivadas se definen tomando el límite de la pendiente de las rectas secantes conforme se van aproximando a la recta tangente.
Es difícil hallar directamente la pendiente de la recta tangente de una función porque sólo conocemos un punto de ésta, el punto donde ha de ser tangente a la función. Por ello, aproximaremos la recta tangente por rectas secantes. Cuando tomemos el límite de las pendientes de las secantes próximas, obtendremos la pendiente de la recta tangente.
Para obtener estas pendientes, tomemos un número arbitrariamente pequeño que llamaremos h. hrepresenta una pequeña variación en x, y puede ser tanto positivo como negativo. La pendiente de la recta entre los puntos  y  es

Esta expresión es un Cociente Diferencial de Newton. La derivada de f en x es el límite del valor del cociente diferencial conforme las líneas secantes se acercan más a la tangente:

Si la derivada de f existe en cada punto x, podemos definir la derivada de f como la función cuyo valor en el punto x es la derivada de f en x.
Puesto que la inmediata sustitución de h por 0 da como resultado una división por cero, calcular la derivada directamente puede ser poco intuitivo. Una técnica es simplificar el numerador de modo que la h del denominador pueda ser cancelada. Esto resulta muy sencillo con funcionespolinómicas, pero para la mayoría de las funciones resulta demasiado complicado. Afortunadamente, hay reglas generales que facilitan la diferenciación de la mayoría de las funciones descritas; ver abajo.
Algunos ejemplos de cómo utilizar este cociente:
Ejemplo 1Consideremos la siguiente función: Entonces: Esta función es constante, para cualquier punto de su dominio vale 5 (por eso f(x+h)=5). Nótese el último paso, donde h tiende a cero pero nunca lo alcanza. Si pensamos un poco, observaremos que la derivada además de ser la pendiente de la recta tangente a la curva, es a la vez, la recta secante a la misma curva.
Ejemplo 2Consideremos la gráfica de 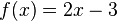. Esta recta tiene una pendiente igual a 2.0 en cada punto. Utilizando el cociente mostrado arriba (junto a los conceptos de límite, secante, y tangente) podremos determinar las pendientes en los puntos 4 y 5: Entonces: Y vemos que se cumple para cualquier número n: Por tanto, se deduce que el valor de la función derivada de una recta es igual a la pendiente de la misma.
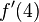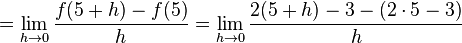Ejemplo 3Mediante esta diferenciación, se puede calcular la pendiente de una curva. Consideremos que: 
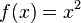
Entonces: 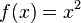Para cualquier punto x, la pendiente de la función  es .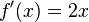

la seguridad:

El término seguridad proviene de la palabra securitas del latín. Cotidianamente se puede referir a la seguridad como la ausencia de riesgo o también a la confianza en algo o alguien. Sin embargo, el término puede tomar diversos sentidos según el área o campo a la que haga referencia.

el riesgo:

es la vulnerabilidad de "bienes jurídicos protegidos" ante un posible o potencial perjuicio o daño para las personas y cosas, particularmente, para el medio ambiente.

el peligro:

es una situación que se caracteriza por la "viabilidad de ocurrencia de un incidente potencialmente dañino", es decir, un suceso apto para crear daño sobre bienes jurídicos protegidos. el peligro es "real" cuando existe aquí y ahora, y es "potencial" cuando el peligro ahora no existe, pero sabemos que puede existir a corto, medio, o largo plazo, dependiendo de la naturaleza de las causas que crean peligro.  

higiene laboral:

se refiere a un conjunto de normas y procedimientos tendientes ala protección de la integridad física y mental del trabajador, preservando de los riesgos de salud inherente a las tareas del cargo y al ambiente físico donde se ejecute.   

imagen sobre la seguridad 

en este vídeo hablan sobre temas básicos de el calculo diferencial y ponen de ejemplo un deporte como lo es el ciclismo.

El cálculo diferencial 

es una parte importante del análisis matemático y dentro del mismo del cálculo infinitesimal. Consiste en el estudio del cambio de las variables dependientes cuando cambian las variables independientes de las funciones o campos objetos del análisis. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial de una función.

En el estudio del cambio de una función, es decir, cuando cambian sus variables independientes es de especial interés para el cálculo diferencial el caso en el que el cambio de las variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace tan pequeño como se desee). Y es que el cálculo diferencial se apoya constantemente en el concepto básico del límite. El paso al límite es la principal herramienta que permite desarrollar la teoría del cálculo diferencial y la que lo diferencia claramente del álgebra.

este vídeo habla sobre la salud ocupacional, que nos habla de ella y para aprender sobre esta carrera ya que estamos estudiando y vamos ser unos profesionales en este tema